02.List（链表）

0、基础理论

链表（Linked List）是一种常见的数据结构，它由一系列节点（Node）组成，每个节点包含两个部分：数据域（Data）和指针域（Pointer）。

单链表，每个节点的指针域都指向下一个节点；
双链表，每一个节点有两个指针域，一个指向下一个节点，一个指向上一个节点。
环形链表，最后一个节点的指针域指向头结点。

节点定义：

public class ListNode {
    int value; // 结点的值
    ListNode next; // 下一个结点
    ListNode prev; // 上一个结点

    public ListNode() {
    }

    public ListNode(int value) {
        this.value = value;
    }

    public ListNode(int value, ListNode next, ListNode prev) {
        this.value = value;
        this.next = next;
        this.prev = prev;
    }
}

1、移除节点

删除链表中等于给定值 val 的所有节点。

示例 1： 输入：head = [1,2,6,3,4,5,6], val = 6 输出：[1,2,3,4,5]
示例 2： 输入：head = [], val = 1 输出：[]
示例 3： 输入：head = [7,7,7,7], val = 7 输出：[]

1.1、设置一个虚拟头结点在进行删除操作

    public static ListNode removeListNode(ListNode head, int target) {
        ListNode mock = new ListNode();
        mock.next = head;

        ListNode node = mock;
        while (node.next != null) {
            if (node.next.value == target) {
                node.next = node.next.next;
            } else {
                node = node.next;
            }
        }
        return mock.next;
    }

1.2、递归删除节点

    public static ListNode removeListNodeRecursion(ListNode head, int target) {
        if (head == null) {
            return null;
        }
        // 假设 removeListNodeRecursion() 返回后面完整的已经去掉val节点的子链表
        // 在当前递归层用当前节点接住后面的子链表
        // 随后判断当前层的node是否需要被删除，如果是，就返回
        // 也可以先判断是否需要删除当前node，但是这样条件语句会比较不好想
        head.next = removeListNodeRecursion(head.next, target);
        if (head.value == target) {
            return head.next;
        }
        return head; // 实际上就是还原一个从尾部开始重新构建链表的过程
    }

2、链表反转

2.1、双指针法

首先定义一个 cur 指针，指向头结点，再定义一个 pre 指针，初始化为 null。然后开始反转，首先要把 cur->next 节点用 tmp 指针保存一下，也就是保存一下这个节点。接下来要改变 cur->next 的指向了，将 cur->next 指向 pre ，此时已经反转了第一个节点了。继续移动 pre 和 cur 指针，循环反转代码逻辑。最后，cur 指针已经指向了 null，循环结束，链表也反转完毕了。此时返回 pre 指针就可以了，pre 指针就指向了新的头结点。

    public static ListNode reverseList(ListNode head) {
        ListNode node = head;
        ListNode prev = null;
        ListNode temp = null;
        while (node != null) {
            temp = node.next;
            node.next = prev;
            prev = node;
            node = temp;
        }
        return prev;
    }

2.2、递归法

从后向前递归链表

    public static ListNode reverseListRecursion(ListNode head) {
        // 边缘条件判断
        if (head == null) {
            return null;
        }
        if (head.next == null) {
            return head;
        }
        // 递归调用，翻转第二个节点开始往后的链表
        ListNode last = reverseListRecursion(head.next);
        // 翻转头节点与第二个节点的指向
        head.next.next = last;
        // 此时的 head 节点为尾节点，next 需要指向 NULL
        head.next = null;
        return last;
    }

3、链表删除倒数第 n 个节点

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

3.1、双指针法

双指针的经典应用，如果要删除倒数第 n 个节点，让 fast 移动 n 步，然后让 fast 和 slow 同时移动，直到 fast 指向链表末尾。删掉 slow 所指向的节点就可以了。具体分为如下几步：

定义 fast 指针和 slow 指针，初始值为虚拟头结点
fast 首先走 n + 1 步，为什么是 n+1 呢，因为只有这样同时移动的时候 slow 才能指向删除节点的上一个节点（方便做删除操作）
fast 和 slow 同时移动，直到 fast 指向末尾
删除 slow 指向的下一个节点

    public static ListNode removeNodeFromTail(ListNode head, int no) {
        //新建一个虚拟头节点指向head
        ListNode mock = new ListNode(Integer.MIN_VALUE, head);
        //快慢指针指向虚拟头节点
        ListNode fast = mock;
        ListNode slow = mock;
        // 只要快慢指针相差 n 个结点即可
        for (int i = 0; i < no + 1; i++) {
            fast = fast.next;
        }
        // 同时移动快慢指针，直到快指针指向链表结尾
        while (fast.next != null) {
            fast = fast.next;
            slow = slow.next;
        }
        // 此时 slow 的位置就是待删除元素的前一个位置
        // 检查 slow.next 是否为 null，以避免空指针异常
        if (slow.next != null) {
            slow.next = slow.next.next;
        }
        return mock.next; // 返回虚拟头结点后的链表
    }

4、链表相交

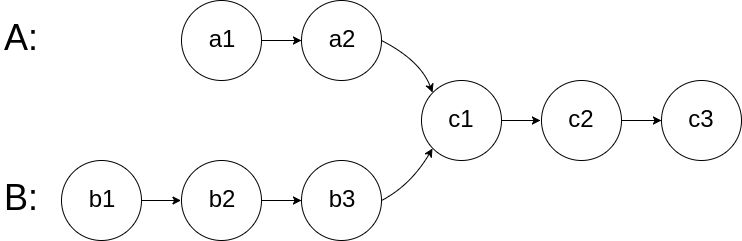
给定两个单链表的头节点 headA 和 headB ，请找出并返回两个单链表相交的起始节点。如果两个链表没有交点，返回 null 。

图示两个链表在节点 c1 开始相交：

链表相交图示

    public static ListNode findIntersectNode(ListNode headA, ListNode headB) {
        int lenA = 0;
        ListNode nodeA = headA;
        while (nodeA != null) {
            lenA++;
            nodeA = nodeA.next;
        }
        int lenB = 0;
        ListNode nodeB = headB;
        while (nodeB != null) {
            lenB++;
            nodeB = nodeB.next;
        }
        // 让nodeA为最长链表的头，lenA为其长度
        if (lenB > lenA) {
            int lenT = lenA;
            lenA = lenB;
            lenB = lenT;
            ListNode nodeT = headA;
            headA = headB;
            headB = nodeT;
        }
        // 求长度差，让nodeA和nodeB在同一起点上（末尾位置对齐）
        nodeA = headA;
        nodeB = headB;
        int step = lenA - lenB;
        while (step-- > 0) {
            nodeA = nodeA.next;
        }
        // 遍历nodeA和nodeB，遇到相同则直接返回
        while (nodeA != null) {
            if (nodeA == nodeB) {
                return nodeA;
            }
            nodeA = nodeA.next;
            nodeB = nodeB.next;
        }
        return null;
    }

5、环形链表

给定一个链表，返回链表开始入环的第一个节点。如果链表无环，则返回 null。

判断链表是否有环

可以使用快慢指针法，分别定义 fast 和 slow 指针，从头结点出发，fast 指针每次移动两个节点，slow 指针每次移动一个节点，如果 fast 和 slow 指针在途中相遇，说明这个链表有环。

这是因为 fast 是走两步，slow 是走一步，fast 指针一定先进入环中，如果 fast 指针和 slow 指针相遇的话，一定是在环中相遇；其实相对于 slow 来说，fast 是一个节点一个节点的靠近 slow 的，所以 fast 一定可以和 slow 重合。

找到环的入口

快慢指针相遇后，再从链表头节点和相遇节点同时出发，直到相遇，相遇点即为环的入口（推导过程有点长，记住结论算了）。

    public static ListNode detectCycle(ListNode head) {
        ListNode fast = head;
        ListNode slow = head;
        while (fast != null && fast.next != null) {
            fast = fast.next.next;
            slow = slow.next;
            // 快慢指针相遇，此时从head和slow相遇点，同时查找直至相遇
            if (fast == slow) {
                // 两个指针，从头结点和相遇结点，各走一步，直到相遇，相遇点即为环入口
                ListNode nodeH = head;
                ListNode nodeF = fast;
                while (nodeF != nodeH) {
                    nodeH = nodeH.next;
                    nodeF = nodeF.next;
                }
                return nodeH;
            }
        }
        return null;
    }

02.List（链表）

0、 基础理论

1、 移除节点